
Publications

Emergent Universal Drag Law in a Model of Superflow
Despite the fundamentally different dissipation mechanisms, many laws and phenomena of classical turbulence equivalently manifest in quantum turbulence. The Reynolds law of dynamical similarity states that two objects of same geometry across different length scales are hydrodynamically equivalent under the same Reynolds number, leading to a universal drag coefficient law. In this work we confirm the existence of a universal drag law in a superfluid wake, facilitated by the nucleation of quantized vortices. We numerically study superfluid flow across a range of Reynolds numbers for the paradigmatic classical hard-wall and the Gaussian obstacle, popular in experimental quantum hydrodynamics. In addition, we provide a feasible method for measuring superfluid drag forces in an experimental environment using control volumes.

Turbulent Relaxation to Equilibrium in a Two-Dimensional Quantum Vortex Gas
M. Reeves et. al
Phys. Rev. X 12, 011031
In this work, we explored the relaxation of initially non-equilibrium configurations of vortices. Impressively, the vortex configurations in equilibrium were found to closely match the predictions of the point vortex model.

Universal dynamics in the expansion of vortex clusters in a dissipative two-dimensional superfluid
Stockdale Oliver R. et al, 2020
Physical Review Research, 2, 3
A large ensemble of quantum vortices in a superfluid may itself be treated as a novel kind of fluid that exhibits anomalous hydrodynamics.

Quantitative Acoustic Models for Superfluid Circuits
Gauthier Guillaume et al, 2019
Physical Review Letters, 123, 26
We experimentally realize a highly tunable superfluid oscillator circuit in a quantum gas of ultracold atoms and develop and verify a simple lumped-element description of this circuit.
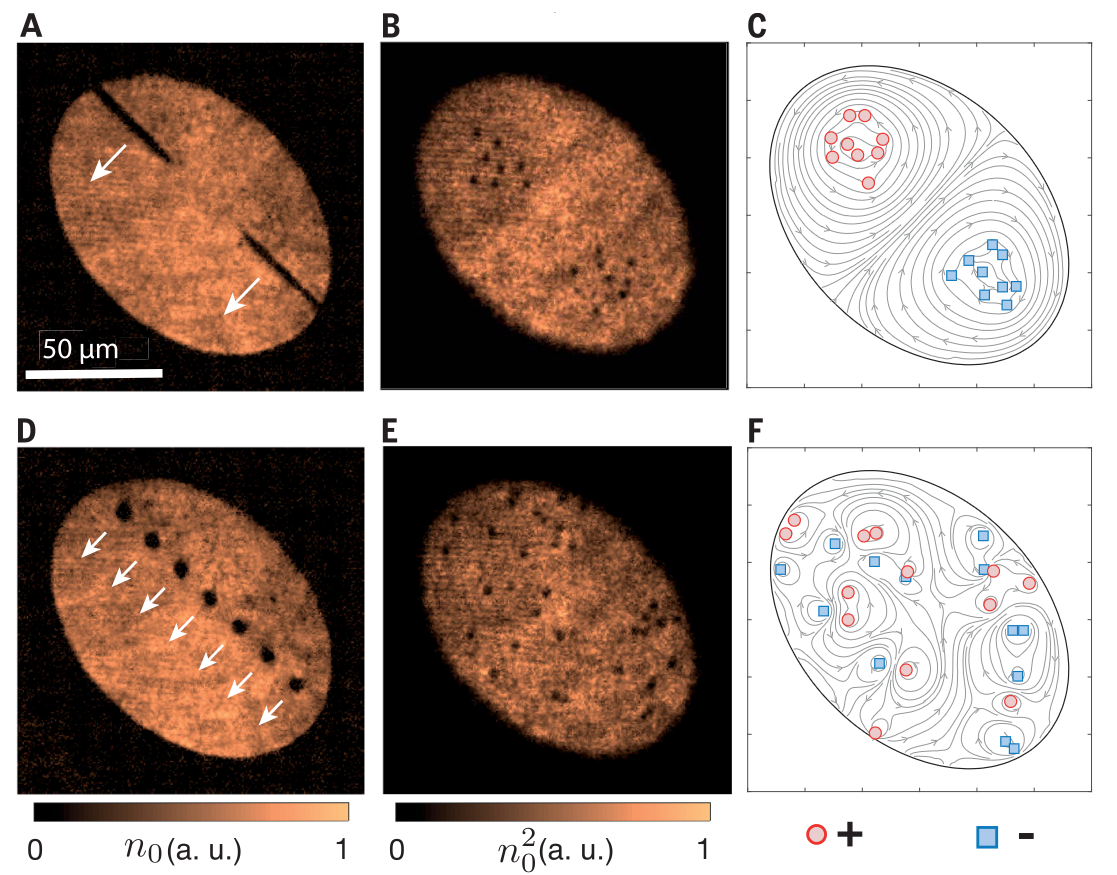
Giant vortex clusters in a two-dimensional quantum fluid
Gauthier Guillaume et al, 2019
Science, 364, 6447, pp. 1264-1267
Adding energy to a system through transient stirring usually leads to more disorder. In contrast, point-like vortices in a bounded two-dimensional fluid are predicted to reorder above a certain energy, forming persistent vortex clusters.
